


Next: Mesh Size Specification
Up: T3d User Guide
Previous: Contents
Model Representation
The model is described by a boundary
representation and consists of the following model entities:
- vertices,
- curves,
- surfaces,
- patches,
- shells, and
- regions.
Topologically, each region is formed by a set of not self-intersecting
boundary surfaces, patches, and shells, each of which is bounded by
a set of curves. Each curve is given by two end vertices. Moreover, each boundary
surface, patch, and shell points out to the regions on the side of its
outer and inner normal. A curve keeps list of surfaces, patches, and
shells sharing that curve. Similarly, a vertex stores the list of curves
sharing that vertex. This basic
topology is further restricted by the geometry of model entities. Both
curves and surfaces are based on free-form representation in terms of
tensor-product polynomial entities. This limits the number of curves
bounding a surface to four. The number of curves bounding a patch or
a shell is not limited (but must be at least two). While the patch is
a planar model entity (trimmed plane), shell is constrained to
a background surface (trimmed surface).
To enhance the modelling capability an
entity-to-entity fixation concept has been introduced. Generally, each model
entity may be fixed to another model entity of the same or higher
dimension. However, the fixed entity is not allowed to coincide with the
boundary of the parent entity. Each
model entity keeps the list of entities fixed to it. No further
topological information is required for the description of a valid
non-manifold domain of almost arbitrary complexity.
Currently, rational Bezier entities are employed for
free-form curves and surfaces representation. This allows to represent
exactly conics and quadrics by entities starting with an order of three
(quadratic curves and biquadratic surfaces).
The rational Bezier curve has the form
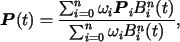 |
(1) |
where
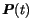 is the point on the curve,
is the point on the curve,
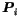 are Bezier control
points,
are Bezier control
points, 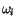 are weights of Bezier control points,
are weights of Bezier control points, 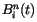 stand for
Bernstein polynomials,
stand for
Bernstein polynomials, 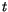 denotes an independent variable varying in
range from
denotes an independent variable varying in
range from 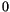 to
to 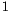 , and
, and 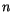 is the curve degree. The curve order is
equal to
is the curve degree. The curve order is
equal to 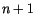 .
.
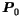 and
and
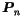 correspond to model vertices while the
remaining points form the control polygon of the curve. They
determine the bow of the curve and need not generally lie on the
curve. The first and last segments of the control polygon coincide
with the curve tangent in the starting and ending vertices respectively.
correspond to model vertices while the
remaining points form the control polygon of the curve. They
determine the bow of the curve and need not generally lie on the
curve. The first and last segments of the control polygon coincide
with the curve tangent in the starting and ending vertices respectively.
The rational Bezier surface can be written in a similar form
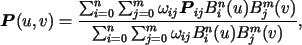 |
(2) |
where
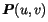 is the point on the surface,
is the point on the surface,
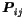 are Bezier control
points,
are Bezier control
points, 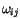 are weights of Bezier control points,
are weights of Bezier control points, 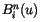 and
and
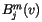 stand for Bernstein polynomials,
stand for Bernstein polynomials, 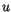 and
and 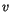 denote
independent parameters varying in range from
denote
independent parameters varying in range from 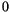 to
to 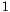 , and
, and 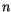 and
and 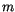 are
surface degrees (orders are equal to
are
surface degrees (orders are equal to 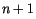 and
and 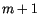 ) in
) in 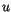 and
and 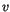 parametric directions, respectively.
If the control points are arranged in a matrix
parametric directions, respectively.
If the control points are arranged in a matrix
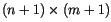 then the
corner points correspond to model vertices, the side points correspond
to control polygons of model curves bounding the surface, and the
remaining points form the control polygon of the surface
and need not generally lie on the surface.
then the
corner points correspond to model vertices, the side points correspond
to control polygons of model curves bounding the surface, and the
remaining points form the control polygon of the surface
and need not generally lie on the surface.
Bernstein polynomial can be expressed as
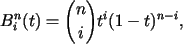 |
(3) |
or recursively as
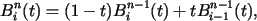 |
(4) |
where 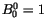 .
.
The ordinary Bezier entities can be derived from
rational Bezier entities when all weights are set to 1.
Two types of model entities are distinguished. The physical ones which
are designated for the actual discretization and the virtual ones which serve as
auxiliary for geometry description or mesh size specification. Note
that there are some restrictions on the fixation between virtual and
physical entities.



Next: Mesh Size Specification
Up: T3d User Guide
Previous: Contents
Daniel Rypl
2008-06-04