
Non-stationary heat transport is described in three-dimensional space. One or two-dimensional problems could be obtained easily by reduction of the sums used in the exposition.
Let a three-dimensional domain Ω be assumed. Coordinates of points in the domain Ω are denoted xi in component notation or x in vector notation. Time is denoted t. The amount of heat which flows through in the normal direction to an unit area (one meter squared) per unit time (one second) is called the heat flux density and is denoted qn(xi,t), where the subscript n indicates the normal direction. The heat flux denisity is expressed in J/(m2s). In a general coordinate system, the density of heat flux is a vector and it is denoted q(x,t). The amount of heat stored in a unit volume is s(x,t) (J/m3).
The heat balance equation has the form


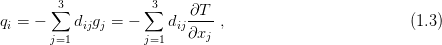

The flux in the direction of a normal vector ni could be expressed with the help of the heat flux density qi in the form
Let boundary of the domain Ω be denoted Γ. The boundary is a union of four parts Γp, Γf, Γt and Γr. Dirichlet boundary condition (prescribed value) is prescribed on Γp, Neumann boundary condition (prescribed flux density) is prescribed on Γf, Newton (Cauchy, Robin) boundary condition (transmission) is prescribed on Γt and radiation boundary condition is prescribed on Γr.For all internal points of the domain Ω, the governing equation has the form
where z denotes the source of heat per unit volume and unit time (J/(m3s)), ρ stands for the density of material (kg/m3) and c expresses the capacity (J/(kg K)). Boundary conditions are in the form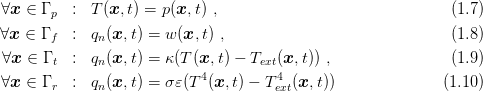
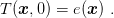 | (1.11) |
The problem has non-homogeneous boundary conditions and will be transformed into problem with homogeneous conditions. The function T is split into two functions
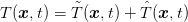 | (1.12) |
which satisfy the following conditions
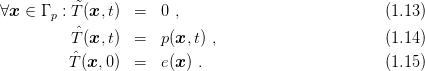

The governing equation (1.6) is multiplied by a test function phi which satisfies the homogeneous Dirichlet boundary conditions and the equation is integrated over the domain Ω (this is Galerkin method). Taking into account also relationship (1.12), the following equation is obtained
The first term of (1.17) can be modified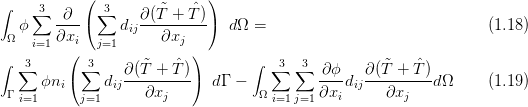
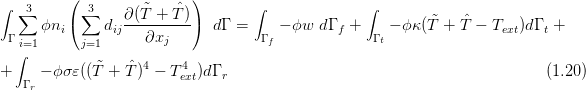
The continuous functions from the previous relations are discretized by the finite element method in the following form
where| d | is the vector of unknown nodal temperatures, |
| e | is the vector of initial temperature in Ω and prescribed temperature on Γp, |
| ϕ | is the vector of nodal values of the test function, |
| w | is the vector of nodal values of prescribed heat flux densities on part Γf, |
| z | is the vector of nodal values of heat source, |
| u | is the vector of nodal values of temperature of external environment prescribed on part Γt, |
| N[d] | is the matrix of basis (approximation) functions for temperature, |
| N[e] | is the matrix of basis (approximation) functions for initial and prescribed temperature, |
| N[ϕ] | is the matrix of basis (approximation) functions for the test function, |
| N[w] | is the matrix of basis (approximation) functions for prescribed heat density flux on Γ f, |
| N[z] | is the matrix of basis (approximation) functions for the heat source, |
| N[u] | is the matrix of basis (approximation) functions for temperature of external environment prescribed on Γ t |
After substitution of the previous approximation (1.22-1.30) to equation (1.21), the following equation is obtained
![∫ (
- ϕT (B [ϕ])TDB [d]d - ϕT(B [ϕ])T DB [e]e + ϕT (N [ϕ])TN [z]z - (1.31 )
Ω ∫
- ϕT (N [ϕ])TρcN [d]d˙- ϕT(N [ϕ])TρcN [e]u ˙)dΩ - ϕT (N [ϕ])T N [w ]wd Γ -
Γ f f
∫ ( T [ϕ]T [d] T [ϕ]T [e] T [ϕ]T [u] )
- ϕ (N ) κN d + ϕ (N ) κN e - ϕ (N ) κN u dΓ t = 0 .
Γ t](transports16x.png)
![(∫ (
ϕT - (B [ϕ])T DB [d]d - (B [ϕ])TDB [e]e + (N [ϕ])TN [z]z-
Ω ∫
[ϕ] T [d]˙ [ϕ] T [e]) [ϕ] T [w]
- (N ) ρcN d - (N ) ρcN ˙e dΩ - Γ f(N ) N wd Γ f- (1.32 )
∫ ( ) )
- (N [ϕ])TκN [d]d + (N [ϕ])TκN [e]e - (N [ϕ])TκN [u]u dΓ t = 0 .
Γ t](transports17x.png)
The following matrices and vectors are defined
The balance equation with the previous notation has the form
![( ) ( )
K [T] + K [Tt] d + C d˙= f[z] - K [e] + K [et] e - C [e]˙e - f[f] + f [t] . (1.43 )](transports19x.png)
![N [d] = N [e] = N [ϕ] = N [z] = N [h] = N [u] . (1.44 )](transports20x.png)
The balance equation with the previous notation (1.45-1.51) has the form
In chapter 1, transport of the heat energy is described. There is a single physical quantity transported (the energy), a single balance equation (the energy balance equation (1.6)) and a single unknown function (the temperature T). In the case of two or more transported physical quantities, the appropriate number of balance equations and unknown functions is needed. Coupled heat and moisture transport is an example of transport of heat energy and mass which could be expressed in the form of moisture. Two unknown functions are used in such models, the temperature and the relative humidity (or volumetric moisture content).
Let a general coupled transport of m physical quantities be assumed in a domain Ω ⊂ Rd which is from the d-dimensional space. The quantities are described by functions v[j](x i,t) which depend on spatial coordinates x (in the vector notation) or xi (in the index notation) and time t. The quantites can be collected in the vector

|| v[2](x, t) ||
v(x, t) = || .. || . (2.1)
( . )
v[m ](x, t)](transports23x.png)
 )
| [2] |
q(x,t) = || q (x,t) || (2.2)
|( ... |)
q[m ](x, t)](transports24x.png)
![[j] [j] [j]
g = grad v (x,t) = ∇v (x,t) , (2.4)
[j] ∂v[j](xk,t)-
gi = ∂xi . (2.5)](transports26x.png)
 )
| [2] |
g(x,t) = || g (x,t) || (2.6)
|( ... |)
g[m ](x, t)](transports27x.png)
The flux densities are related with the gradients of the physical quantities by the constitutive relationships. In linear case, the flux densities have the form
Each constitutive matrix D[jk] contains d rows and d columns. The components of D[jk] are called conductivity coefficients. The constitutive relationships (2.7) can be written in the compact vector–matrix form
![( [11] [12] [1m ] )
| D D ... D |
|| D [21] D [22] D [2m ] ||
D = || .. .. .. || . (2.10 )
( .[m1] [m2 ] . .[mm ] )
D D ... D](transports30x.png)
Balance equation for the j-th variable has the form
where z[j] denotes the source of the j-th quantity in a unit volume per unit time and s[j] denotes the amount of the j-th quantity stored in a unit volume. The s[j] can be written in the form where h[jk] are called capacity coefficients.Substitution of (2.8) and (2.14) to the balance equations (2.12) results in the form
The balance equations are accompanied by initial and boundary conditions. The initial conditions have the form
![[j] [j]
v (xi,0) = v0 (xi) . (2.17 )](transports35x.png)
![( )
v[e1]xt(x, t)
|| [2] ||
vext(x, t) = || vext(x, t)|| (2.22 )
|( ... |)
[m]
vext(x, t)](transports38x.png)
![( )
κ[j1]
|| κ[j2] ||
κ [j] = || . || . (2.23 )
( .. )
κ [jm]](transports39x.png)
![[j] [j] ( [j])T
∀x ∈ Γt : qn (x,t) = κ (v (x, t) - vext(x,t)) . (2.24 )](transports40x.png)
The Dirichlet boundary conditions are generally non-homogeneous and therefore the functions v[j](x,t) has to be split into
where the function ṽ[j](x,t) satisfies the homogeneous Dirichlet boundary conditions while the function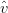 [j](x) satisfies the non-homogeneous Dirichlet boundary conditions.
[j](x) satisfies the non-homogeneous Dirichlet boundary conditions.
![∀x ∈ Γ [j] : v˜[j](x, t) = p [j](x, t) , (2.26 )
p
∀x ∈ Γ [pj] : vˆ[jn] (x, t) = 0 , (2.27 )
[j] [j]
∀x ∈ Ω : v˜n (x, 0) = v0 (x) . (2.28 )](transports43x.png)
![[j] [j] [j]
∀x ∈ Γp : p (x, 0) = v0 (x ) . (2.29 )](transports44x.png)
Multiplication of the j-th balance equation (2.16) by a test function ϕ[j] which satisfies homogeneous Dirichlet boundary conditions, integration over the domain Ω (Galerkin method) and substitution of (2.25) leads to the form
The term on the left side can be modified with the help of Green theorem![∫ i∑=d ∂ k=∑m r∑=d ∂ (˜v [k] + ˆv[k](x ,t))
ϕ[j] ---- D [ijrk]-------------s----dΩ = (2.31 )
Ω i=1∂xi k=1 r=1 ∂xr
∫ i∑=d k∑=m r=∑d [k] [k]
ϕ[j] ni D [jirk]∂(˜v--+--ˆv--(xs,t))d Γ -
Γ i=1 k=1 r=1 ∂xr
∫ i∑=dk∑=m r∑=d [j] [k] [k]
- ∂-ϕ--D [jirk]∂(˜v---+-ˆv--(xs,t))dΩ .
Ω i=1k=1 r=1 ∂xi ∂xr](transports46x.png)
![∫ i=∑d k=∑m r∑=d [k] [k]
ϕ [j] ni D[ijrk]∂-(˜v--+-ˆv--(xs,t))dΓ = (2.32 )
Γ i=1 k=1r=1 ∂xr
∫ i=∑d ∫ ∑i=d
= - ϕ [j] niq[ij]dΓ [j]- ϕ[j] niq[ji] d Γ [jt]=
Γ [fj] i=1 f Γ [jt] i=1
∫ ∫ i=∑m
= - ϕ[j]w[j]dΓ [j]- ϕ [j] κ [ji](˜v[i] + ˆv[i] - v[ie]xt)dΓ [jt].
Γ [jf] f Γ [tj] i=1](transports47x.png)
The continuous functions from the previous relations are discretized by the finite element method in the following form
where| d[j] | is the vector of unknown nodal values of the j-th quantity, |
| e[j] | is the vector of initial nodal values of the j-th quantity in Ω and prescribed values of the j-th quantity on Γ p, |
| ϕ[j] | is the vector of nodal values of the j-th test function, |
| w[j] | is the vector of nodal values of prescribed flux densities of the j-th quantity on part Γ f, |
| z[j] | is the vector of nodal values of source of the j-th quantity, |
| u[j] | is the vector of nodal values of the j-th quantity of external environment prescribed on part Γ t, |
| N[j,d] | is the matrix of basis (approximation) functions for the j-th quantity, |
| N[j,e] | is the matrix of basis (approximation) functions for initial and prescribed values of the j-th quantity, |
| N[j,ϕ] | is the matrix of basis (approximation) functions for the j-th test function, |
| N[j,w] | is the matrix of basis (approximation) functions for prescribed density flux of the j-th quantity on Γ f, |
| N[j,z] | is the matrix of basis (approximation) functions for the source of the j-th quantity, |
| N[j,u] | is the matrix of basis (approximation) functions for the j-th quantity of external environment prescribed on Γ t. |
After some manipulations, the equation (2.33) can be written in the form
Approximation functions for continuous functions are usually identical, therefore the following relationship is valid
![N [d] = N [e] = N [ϕ] = N [z] = N [h] = N [u] . (2.44 )](transports51x.png)
![( K [11] K [12] ... K [1m ])
|| t[21] t[22] t[2m ]||
K = || K t K t K t || , (2.54 )
t | ... ... ... |
( [m1 ] [m2] [mm ])
K t K t ... K t](transports55x.png)
![( )
C [11] C [12] ... C [1m]
|| C [21] C [22] C [2m] ||
C = || . . . || , (2.55 )
|( .. .. .. |)
C [m1] C [m2] ... C [mm ]](transports56x.png)
![( [1] [1] [11] [12] [1m] )
| fz - ff + ft + ft + ...+ f t |
|| f[z2]- f[f2]+ f[t21] + f[t22]+ ...+ f [2tm] ||
f = || .. || , (2.56 )
( . )
f [mz] - f[fm]+ f[tm1]+ f [mt2]+ ...+ f [mtm ]](transports57x.png)
![( [1] )
| d |
|| d[2] ||
d = || .. || , (2.57 )
( .[m] )
d](transports58x.png)
![( ˙[1] )
| d |
|| ˙d[2] ||
˙d = || .. || , (2.58 )
|( . |)
˙d[m]](transports59x.png)
![( e[1])
| [2]|
e = || e || , (2.59 )
|( ... |)
[m ]
e](transports60x.png)
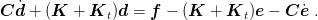
Künzel model is an example of heat energy and mass (moisture) transport. The physical quantities used in the model are the relative humidity φ (dimensionless) and the temperature T (K).
The relative humidity is limited to the interval ⟨0; 1⟩. It is defined

Moisture content w (m3/m3) is defined in the form
where V w is the volume of moisture in pores of the representative specimen while V is the volume of the whole specimen. For the relative humidity from the interval ⟨0; 0, 97⟩, the accumulation function is called the sorption isotherm and it is in the form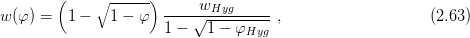
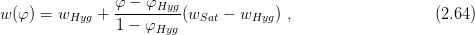
Cappilary water transport coefficient Dw is defined in the form




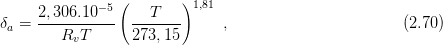
faktor difúzního odporu vodní páry μ z intervalu ⟨1; ∞⟩
Water vapour permeability has the form


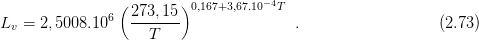
The mass balance equation (balance equation for moisture) has the form
![∂ρv- [φφ] [φT]
∂t = div(D ∇ φ + D ∇T ) , (2.74 )](transports76x.png)
![∂H
----= div(D[TT]∇T + D [T φ]∇ φ ) . (2.75 )
∂t](transports77x.png)
Time derivative of the enthalpy density is

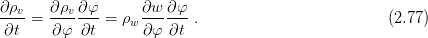
Moisture flux density has the form
![dp
q [φ] = (D ϕ + δpps)∇ φ + δpφ--s∇T , (2.78 )
dT](transports80x.png)
![[T] dps-
q = (λ + Lvδpφ dT )∇T + Lvδpps∇ φ (2.79 )](transports81x.png)
The moisture balance equation is in the form
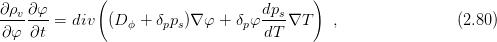
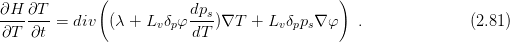
Vector of the physical quantities has the form

![( )
g[φ]
g = g[T] , (2.83 )](transports85x.png)
![( )
q[φ]
q = q[T] , (2.84 )](transports86x.png)
![( D [φφ] D [φT ])
D = [Tφ ] [TT ] , (2.85 )
D D](transports87x.png)
![( )
H [φ φ] H [φT]
H = H [T φ] H [TT] . (2.86 )](transports88x.png)
The balance equations have the form
![[φφ]∂φ- [φφ] [φ [φT] [T]
H ∂t = div(D g ]) + div(D g ) , (2.87 )
∂T
H [TT]--- = div(D [Tφ]g[φ]) + div(D [TT]g[T]) . (2.88 )
∂t](transports89x.png)
Components of the capacity matrix of material are
![∂ϱv
H [φφ] = ----, (2.89 )
∂ φ
H [φT] = 0 , (2.90 )
[Tφ]
H = 0 , (2.91 )
H [T T] = ∂H-- (2.92 )
∂T](transports90x.png)
![[φφ]
D = D ϕ + δpps , (2.93 )
[φT] dps-
D = δpφ dT , (2.94 )
[Tφ]
D = Lv δpps , (2.95 )
[TT] dps-
D = λ + Lv δpφdT . (2.96 )](transports91x.png)
The unknown function are discretized in the form
![φ = N [φ]d [φ] , (2.97 )
[T] [T ]
T = N d , (2.98 )](transports92x.png)
![η[φ] = N [φ]b [φ] , (2.99 )
η[T] = N [T]b[T] , (2.100 )](transports93x.png)
![g[φ] = B [φ]d [φ] , (2.101 )
[T] [T] [T]
g = B d . (2.102 )](transports94x.png)
![[φφ]˙[φ] [φφ] [φ] [φT] [T]
C d + K d + K d = 0 , (2.103 )
C [TT]˙d[T] + K [Tφ]d[φ] + K [TT]d[T] = 0 . (2.104 )](transports95x.png)
![( )( [φ] ) ( )( ) ( )
C [φφ] 0 ( ˙d ) K [φφ] K [φT] d[φ] 0
0 C [TT] ˙[T] + K [Tφ] K [TT] d[T] = 0 . (2.105 )
d](transports96x.png)
List of quantities used in the model:
Relationships used in the model
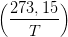 0,167+3,67.10-4T the latent heat of evaporation of water
(J/kg)
0,167+3,67.10-4T the latent heat of evaporation of water
(J/kg)
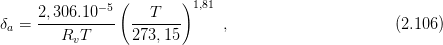
faktor difúzního odporu vodní páry μ z intervalu ⟨1; ∞⟩
Permeabilita vodní páry (water vapour permeability)

The balance equations
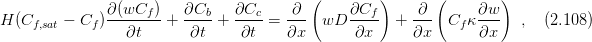
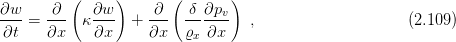
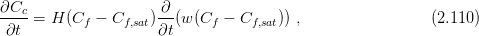
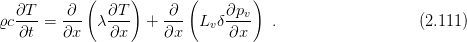
The balance equations modified with respect to computer implementation. The balance equation for moisture (mass)
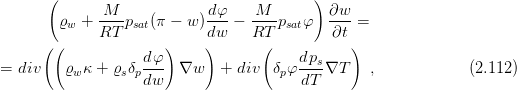
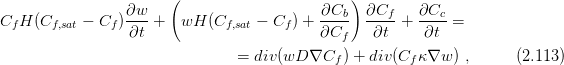
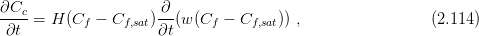
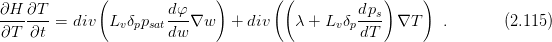
The vector of physical quantities

![( [w])
| g[f]|
g = || g || , (2.117 )
( g[c])
g[T]](transports109x.png)
![( )
q[w]
|| q[f]||
q = |( q[c]|) , (2.118 )
[T]
q](transports110x.png)
![( )
D [ww ] D [wf] D [wc] D [wT ]
|| D [fw ] D [ff] D [fc] D [fT] ||
D = |( [cw] [cf] [cc] [cT] |) , (2.119 )
D [T w] D [Tf] D [Tc] D [TT ]
D D D D](transports111x.png)
![( [ww ] [wf] [wc] [wT])
| H [fw ] H [ff] H [fc] H [fT]|
H = || H H H H || . (2.120 )
( H [cw] H [cf] H [cc] H [cT])
H [T w] H [Tf] H [Tc] H [TT]](transports112x.png)
![[ww]∂w- [ww] [w] [wT ] [T]
H ∂t = div (D g + div(D g ) , (2.121 )
∂w ∂Cf ∂Cc
H [fw]--- + H [ff]---- + H [fc]---- = div (D [fw]gw ]) + div(D [ff]g[f]) , (2.122 )
∂t ∂t ∂t
H [cw]∂w-+ H [cf]∂Cf- + H [cc]∂Cc- = 0 , (2.123 )
∂t ∂t ∂t
[TT]∂T [Tw] [w ] [TT ][T]
H ∂t- = div (D g ) + div(D g ) . (2.124 )](transports113x.png)
The components of capacity matrix of material
![[ww] M--- dφ- M---
H = ϱw + RT psat(π - w )dw - RT psatφ , (2.125 )
[wf]
H = 0 , (2.126 )
H [wc] = 0 , (2.127 )
H [wT] = 0 , (2.128 )](transports114x.png)
![[fw]
H = Cf H (Cf,sat - Cf) , (2.129 )
[ff] ∂Cb-
H = wH (Cf,sat - Cf) + ∂C , (2.130 )
f
H [fc] = 1 , (2.131 )
H [fT] = 0 , (2.132 )](transports115x.png)
![[cw]
H = - (Cf - Cf,sat)H (Cf - Cf,sat) , (2.133 )
H [cf] = - wH (Cf - Cf,sat) , (2.134 )
[cc]
H = 1 , (2.135 )
H [cT] = 0 , (2.136 )](transports116x.png)
![[Tw]
H = 0 , (2.137 )
H [Tf] = 0 , (2.138 )
[Tc]
H = 0 , (2.139 )
[TT] ∂H--
H = ∂T , (2.140 )](transports117x.png)
![[ww ] dφ
D = ϱwκ + ϱsδp dw-, (2.141 )
[wf]
D = 0 , (2.142 )
D [wc] = 0 , (2.143 )
dp
D [wT ] = δpφ --s-, (2.144 )
dT](transports118x.png)
![D [fw ] = Cfκ , (2.145 )
[ff]
D = wD , (2.146 )
D [fc] = 0 , (2.147 )
D [fT ] = 0 , (2.148 )](transports119x.png)
![D [cw] = 0 , (2.149 )
[cf]
D = 0 , (2.150 )
D [cc] = 0 , (2.151 )
[cT]
D = 0 , (2.152 )](transports120x.png)
![D [T w] = k δ p dφ-, (2.153 )
v p satdw
D [Tf] = 0 , (2.154 )
[Tc]
D = 0 , (2.155 )
[T T] dps
D = λ + Lvδp dT--, (2.156 )](transports121x.png)
neznámé veličiny
![[w] [w]
w = N d (2.157 )
Cf = N [f]d[f] (2.158 )
[c] [c]
Cc = N d (2.159 )
T = N [T]d[T] (2.160 )](transports122x.png)
![[w ] [w] [w]
η = N b (2.161 )
η[f] = N [f]b[f] (2.162 )
η[c] = N [c]b[c] (2.163 )
[T]
η[T ] = N [T]b (2.164 )](transports123x.png)
![g[w] = B [w ]d [w] (2.165 )
[f] [f] [f]
g = B d (2.166 )
g [c] = B [c]d[c] (2.167 )
[T] [T ][T]
g = B d (2.168 )
(2.169 )](transports124x.png)
![[ww] [w] [ww] [w] [wT] [T]
C ˙d + K d + K d = 0 (2.170 )
[fw ]˙[w] [ff]˙[f] [fc]˙[c] [fw] [w ] [ff] [f]
C d + C d + C d + K d + K d = 0 (2.171 )
C [cw]˙d[w] + C [cf]˙d[f] + C [cc]d˙[c] = 0 (2.172 )
[T]
C [TT]˙d + K [Tw]d[w] + K [TT]d[T] = 0 (2.173 )](transports125x.png)
![( ) ( [w] ) ( ) ( )
C [ww] 0 0 0 | d˙ | K [ww] 0 0 K [wT] d [w] ( 0 )
|| C [fw] C [ff] C [fc] 0 || || d˙[f] || || K [fw] K [ff] 0 0 || || d [f] || | 0 |
|| [cw] [cf] [cc] || || [c] || + || || || [c] || = || ||(2..174 )
( C C C 0 ) |( d˙ |) ( 0 0 0 0 ) ( d ) ( 0 )
0 0 0 C [TT] d˙[T] K [Tw] 0 0 K [TT] d [T] 0](transports126x.png)
Parabolic problems after space discretization lead to systems of ordinary differential equations in the form
where d(t) is the vector of nodal unknowns and f(t) is the vector of given right hand side. In the case of transport processes, f(t) denotes the prescribed fluxes, K is the conductivity matrix and C is the capacity matrix.The vector of nodal values d evaluated at time instant i + 1 is assumed in the form
where the vector vi+α has form The vector v contains time derivatives of unknown nodal variables, i.e. time derivatives of the vector d. Substitution of expressions (3.2) and (3.3) to the equation (3.1) results in This formulation is suitable because explicit or implicit computational scheme can be set by parameter α. Advantage of the explicit algorithm is based on possible efficient solution of the system of equations because parameter α can be equal to zero and capacity matrix C can be diagonal. Therefore the solution of the system is extremely easy. The disadvantage of such method is its conditional stability. It means, that the time step must satisfy stability condition what usually leads to very short time step.In order to abbreviate notation, predictor is defined in the form

In the case αΔt≠0, the vector vi+1 can be expressed from (3.7) in the form

| Initial vectors | d0,v0 | |
| (defined by initial conditions) | ||
| do until | i ≤ n | |
| (n is the number of time steps) | ||
| predictor | 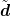 i+1 = di + (1 - α)Δtvi i+1 = di + (1 - α)Δtvi |
|
| right hand side vector | yi+1 = fi+1 -K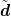 i+1 i+1 |
|
| matrix of the system | A = C + αΔtK | |
| solution of the system | vi+1 = A-1y i+1 | |
| new approximation | di+1 = 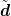 i+1 + αΔtvi+1 i+1 + αΔtvi+1 |
|
| Initial vectors | d0,v0 | |
| (defined by initial conditions) | ||
| do until | i ≤ n | |
| (n is the number of time steps) | ||
| predictor | 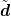 i+1 = di + (1 - α)Δtvi i+1 = di + (1 - α)Δtvi |
|
| right hand side vector | yi+1 = αΔtfi+1 + C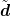 i+1 i+1 |
|
| matrix of the system | A = C + αΔtK | |
| solution of the system | di+1 = A-1y i+1 | |
| new approximation | vi+1 = 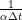 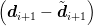 |
|