MR.BEAM PROJECT

KEYWORDS (general): civil engineering, optimization
KEYWORDS (specific):  reinforced concrete, continuous beam, design


 
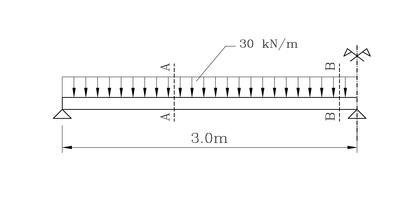
In present, empiric formulas are commonly used by civil engineers to design reinforced concrete structures and structural elements. This approach gives a possibility to design an element to be best fitted to given load, but does not take under consideration economic and practical point of view - this means that element designed in such a way is not the cheapest one and the most simple to built. Our target was to find the best possible fashion of a structure with minimal price and maximum buildability. As was pointed out, using effective optimization method together with economic criterias can substantialy reduce expended costs necessary to build this type of structure. We have studied this problem on a specific example: a reinforced concrete beam under a certain loading state (see Fig. 1). 
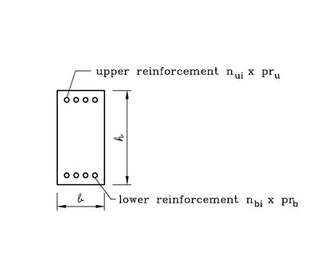
Figure 1: An example of a continuous beam
After some years I was working on this project and after comparison with other approaches how to design reinforced concrete beams I have recognised that it is necessary to implement a diameter of reinforcement bars into an analysis model. An ussual concept is to compute steel area only but this design disagree with a final situation. The problem is that in case of constant steel area and different types of bars an ultimate moment can vary. Than the ussual way of designing leads to a non-efficient state. It is not also suitable to change diameters within one cross-section because of buildability. Hence, I have recognized that the most simple way is to have the same types of bars along the top and the bottom of a beam (see Fig. 2). 
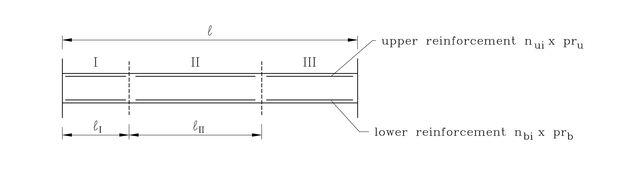
Figure 2: A typical beam cross-section
The next step is a division of a beam between two supports into three parts ( Fig. 3). It is due to a typical distribution of bending moments along the span in frames. I firstly implemented this independently in 1999 but I have recornized that this approach was earlier used for example in [2] in 1996. On the other hand I am using discrete values (distances taken from FEM) of sections not continuous as authors in the reference.
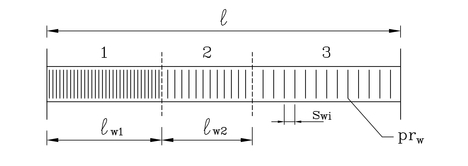
Figure 3: Beam sections between supports
The same strategy is used on shear reinforcement (Fig. 4). A diametr of stirrups is same along a beam. A spacing between stirrups can vary in appropriate sections.
Figure 4: Beam sections with shear reinforcement
A summation - there are 18 unknowns in the example: cross-section dimensions b and h, diameters pru and prb, 3x count of bars in each section nui and nbi, lengths of moment sections lI and lII, a diameter of stirrups prw, lengths of shear sections lwI and lwII, and finaly 3 spacings of stirrups swi. All variables are integers or discrete numbers from real domains. 

The aim is to minimize the overall price of this structure. The objective function is a linear combination of a weight of steel and a volume of concrete multiplied by appropriete prices. Constraints according to Eurocode 2 standards are included as a penalty function. Conditions for ultimate limit state (bending and shear bearing capacity) and serviceability limit state (maximum allowable deflection) are included.
Is this function really difficult to optimize?

I have tried Monte Carlo method to check a behavior of this function and I think results is enough expressive. Note, that the best price ever found is 573.50 CZK.
Number of solutions
  Comment
9 007 199 254 740 992 
  Amount of all possible solutions
100 000 000 
  Monte Carlo trials
24 698 222 
  Feasible solutions
722 
  Solutions with price under 1000 CZK
55 
  With price under 900 CZK
0 
  With price under 800 CZK


To solve this problem several optimization method have been used:

BASA - binary augmented simulated annealing
DE- differential evolution

References:

    [1] Matej Leps & Michal Sejnoha: New approach to optimization of reinforced concrete beams, Computational Concrete Structures Technology, Civil-Comp Press, 2000
    [2] Komousis, V.K., Arsenis, S.J., Vasiloglu, V.B.: Detailed design of reinforced concrete buildings using logic programming, Advances in Engineering Software, Vol. 25, 1996

Authors:

     Matej Leps email:<matej.leps@fsv.cvut.cz> hmpg:http://klobouk.fsv.cvut.cz/~leps
     Ondra Hrstka email:<ondra@klobouk.fsv.cvut.cz> hmpg:http://klobouk.fsv.cvut.cz/~ondra