|
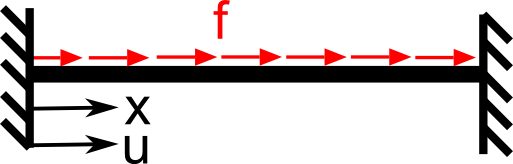
1. otázka: Pro příklad na obrázku vyjádřete slabou formulaci úlohy
{\color{blue} EA \frac{\mathrm{d}^2u(x)}{\mathrm{d}x^2} + f(x) = 0}
včetně určení definičních oborů (příslušných prostorů funkcí).
|
|
a)
{\color{blue} u \in H^1(0,L), \quad v \in H^1(0,L)},
{\color{blue} a(u,v) = \int\limits_0^L \frac{\mathrm{d}v}{\mathrm{d}x} EA \frac{\mathrm{d}u}{\mathrm{d}x} \mathrm{d}x, \quad
F(v) = \int\limits_0^L f v \mathrm{d}x,\quad
a(u,v) = F(v)}
b) {\color{blue} u \in H^1(0,L), \quad v \in H^1(0,L)},
{\color{blue} a(u,v) = \int\limits_0^L v EA \frac{\mathrm{d}^2u}{\mathrm{d}x^2} \mathrm{d}x, \quad
F(v) = \int\limits_0^L f v \mathrm{d}x,\quad
a(u,v) = F(v)}
c) {\color{blue} u \in H^1(0,L), \quad v \in H^1(0,L)},
{\color{blue} a(u,v) = \int\limits_0^L v EA \frac{\mathrm{d}^2u}{\mathrm{d}x^2} \mathrm{d}x, \quad
F(v) = \int\limits_0^L f \mathrm{d}x,\quad
a(u,v) = F(v)}
d) nevím |
|
2. otázka: Konstrukci na obrázku diskretizujte lineárními prvky délky h = L/3.
Uvažujte normálovou tuhost průřezu EA = 1 MN, délku nosníku L = 2 m a intenzitu spojitého zatížení f = 1 kN/m.
Vypočtěte chybu řešení {\color{blue} e_h = u-u_h}, kde {\color{blue}u} je přesné a {\color{blue}u_h} je přibližné řešení, měřenou v normě
{\color{blue} \lvert\lvert e_h \rvert\rvert_0= \sqrt{\int\limits_0^L e_h^2(x)\mathrm{d}x}}
|

|
a) {\color{blue} 5.1378\times10^{-4}}
b) {\color{blue} 5.2378\times10^{-4}}
c) {\color{blue} 5.3378\times10^{-4}}
d) {\color{blue} 5.4378\times10^{-4}}
e) {\color{blue} 5.5378\times10^{-4}}
f) nevím |
|
3. otázka: Jak by se změnila chyba řešení z předchozího příkladu, pokud by byl nosník diskretizován 300 prvky (stejné délky h = L/300)?
|
a) chyba řešení zůstane stejná
b) chyba řešení se zmenší {\color{blue} 10\times\:}
c) chyba řešení se zmenší {\color{blue} 100\times\:}
d) chyba řešení se zmenší {\color{blue} 1000\times\:}
e) chyba řešení se zmenší {\color{blue} 10000\times\:}
f) nevím |
|
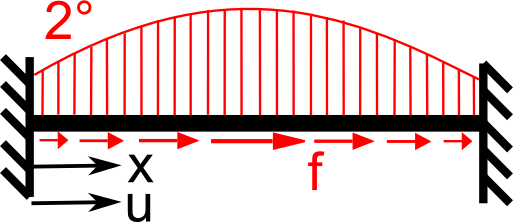
4. otázka: Uvažujme Abstraktní variační problém (AVP) {\color{blue} a(u,v) = F(v) \quad \forall v \in V} pro 1D úlohu na obrázku.
Jakého řádu konvergence bude chyba {\color{blue} ||u - u_h||_{0,\Omega}}
( {\color{blue}u} je přesné a {\color{blue}u_h} je přibližné řešení), když použijeme lineární prvky.
|
|
a) {\color{blue} h}
b) {\color{blue} h^2}
c) {\color{blue} h^3}
d) {\color{blue} h^4}
e) {\color{blue} h^5}
f) nevím |
5. otázka: Nechť {\color{blue} u} je řešení AVP, {\color{blue} a(u,v)=\int_{-1}^1 u' v' \mathrm{d}x,\:\:
F(v)=\int_{-1}^1 fv \mathrm{d}x}.
Vyberte {\color{blue} u_h \in V_h}, {\color{blue} V_h \subset V}, pokud
{\color{blue} u = \frac{x^3}{2}}.
Nápověda: použijte Galerkinovskou ortogonalitu.
|
a) {\color{blue} x^2}
b) {\color{blue} \cos(x)}
c) {\color{blue} 5-x/2}
d) {\color{blue} x^3 +2x}
e) nevím |