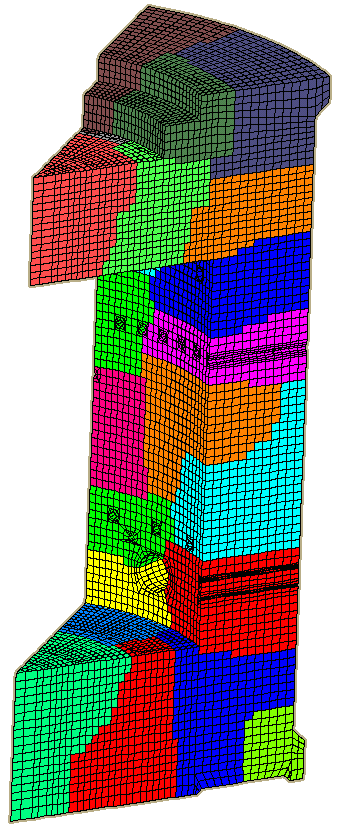
SIFEL Home page
SIFEL Home page
SIFEL - SImple Finite ELements
Extension of MEFEL code
All the source files of MEFEL are available and therefore the MEFEL can be extended in any area of mechanical problem. The most common cases of the code extension represent implementation of new material model and implementation of new finite element.
Implementation of new material model
The main procedures of any material model in the code represent evaluation of correct stresses for trial strains and assembling of the matrix of stiffness coefficients, D. These computations are performed at every integration point of all elements where the strains and stresses are stored and actualized by any solver implemented in the code. The material models are implemented with help of C++ classes where one material model is represented by one class type. Every class of material model must contain the following compulsory functions:
void newmaterial::read (XFILE *in);- reads necessary data of the model, in is pointer to the input file,void newmaterial::matstiff (matrix &d, long ipp, long ido)- assembles the stiffness matrix D, the resulting stiffness matrix have to be stored in the argumentd,ippdenotes the number of integration point,idostands for the index in arraysother/eqother,void newmaterial::nlstresses (long ipp, long im, long ido)- computes correct stresses for actual strains,ippdenotes the number of integration point,imexpresses the index of material model at the integration point andidostands for the index in arraysother/eqother,void newmaterial::updateval (long ipp, long im, long ido)- updates all internal material variables when the equilibrium is attained,ippdenotes the number of integration point,imexpresses the index of material model at the integration point andidostands for the index in arraysother/eqother.
read procedure. For example, elastic
isotropic material model needs to read two parameters - Young modulus and Poisson's ratio and it stores
them in the class data members elisomat::e and elisomat::nu
(see MEFEL/SRC/elastisomat.h|cpp)
Integration points play significant role in the code. They contain information about used
material models, strains and stresses, internal material variables etc. All integration points are stored
in the global variable Mm of mechmat class. The mechmat
class contains data member ip which represents array of all integration points.
At integration point, the following data members are defined:
tm- array that contains type of material(s),idm- array that contains identification number of material(s),stress- array of stress components actualized by material model,strain- array of strain components actualized by solver,ncompstr- number of components of the above stress and strain arrays,other- contains all internal material parameters/variables, which are not in the equilibrium during the iteration (allocated only for nonlinear models),eqother- contains equilibrated internal material parameters/variables stored in the array (allocated only for nonlinear models),nonloc- array of nonlocal averaged values (allocated only for nonlocal material models).
For example, if the material class needs to obtain actual strains at beginning of stress calculation
(newmat::nlstresses), it can be done with help of the following statements:
long ncompstr = Mm->ip[ipp].ncompstr; // get number of stress/strain components
vector eps(ncompstr); // create auxiliary vector for strain storage
for(long i=0; i<ncompstr; i++)
eps(i) = Mm->ip[ipp].strain[i]; // store individual strain components to eps
for loop can be replaced by the call of mechmat procedure
Mm->givestrains(0, ipp, eps). Similarly, the resulting stress components have to be stored at the end of
stress computation in stress array and it can be provided by the following code:
long ncompstr = Mm->ip[ipp].ncompstr; // get number of stress/strain components
vector sig(ncompstr); // create auxiliary vector for stress storage
.
. // code for stress computation
.
for(long i=0; i<ncompstr; i++)
Mm->ip[ipp].stress[i] = sig(i); // store individual strain components to eps
for loop can be replaced by the call of mechmat procedure
Mm->storestress(0, ipp, sig).
Integration points have the stress and strain components stored as vectors in engineering notation. The order of stress/strain components in the vector is defined with respect to stress/strain states as follows:
- 1D - sig = {sig_x}
- 2D plane strain/stress - sig = {sig_x, sig_y, tau_xy, sig_z}^T, eps = {eps_x, eps_y, gamma_xy, eps_z}^T
- Axisymmetric problem - sig = {sig_x, sig_y, sig_z, tau_xy}^T, eps = {eps_x, eps_y, eps_z, gamma_xy}^T
- 3D - sig = {sig_x, sig_y, sig_z, tau_yz, tau_xz, tau_xy}^T, eps = {eps_x, eps_y, eps_z, gamma_yz, gamma_xz, gamma_xy}^T
Arrays other/eqother contains all internal material variables needed in nonlinear material models while the
elastic models do not use them. For example, plastic models require to store plastic strains, consistency parameter and optionally
hardening parameters, damage models require to store damage parameter, etc. These internal parameters/variables, that are
not constant for particular integration points, should be stored in eqother/other arrays. The meaning and the order of parameters
in the array other/eqother are defined by the given material model. The number of eqother/other array components must be
specified in switch statements of mechmat::givencompother and mechmat::givencompeqother
(see MEFEL/SRC/mechmat.h|cpp) functions. Typically in case of plasticity models, the plastic strains from the last equilibrium
step are loaded from the Mm->ip[ipp].eqother array and at the end of stress computation, new plastic
strains are stored in the Mm->ip[ipp].other array. In both cases, components of
other/eqother arrays must be accessed with help of shift index ido which
is provided in the argument list of functions:
long ncompstr = Mm->ip[ipp].ncompstr; // get number of stress/strain components
The
vector eps_p(ncompstr);
for (long i=0; i<ncompstr; i++)
eps_p[i] = Mm->eqother[ido+i]; // use plastic strains from the previous step
.
. // code for stress computation
.
for (long i=0; i<ncompstr; i++)
Mm->other[ido+i] = eps_p[i]; //storage of new plastic strains
newmat::updateval function is called by solver at the end of each time step if the equilibrium
was attained. In this function, the values of other array have to be copied to the eqother array at
the given integration point.
The reading of material constants should be performed in the newmat::read function. The argument of the
function is the pointer to the opened text file defined by XFILE structure and the file position pointer
is expected to be set at the beginning of the material record. The material constants have to be read by xfscanf
function which is similar to the fscanf function defined in standard C library. The first argument is
the pointer to the XFILE, the second is the format string. This format may contain conversion specifications;
the results from such conversions, if any, are stored in the locations pointed to by the pointer arguments that follow format.
Each pointer argument must be of a type that is appropriate for the value returned by the corresponding conversion specification.
The format string accepts all common conversion specifiers as the fscanf function but there are three
conversions added/redefined - %a, %k and %m. They are used for the reading of text block (%a), keyword string (%k) and
enum type (%m).
The function newmat::matstiff should assemble material stiffness matrix according to the solver requirements.
The type of matrix (initial, tangent, secant, ...) is given in the global variable Mp of
probdesc type which holds all data about the problem description. The type of stiffness matrix is determined
by data member Mp->stmat which is of enum type stiffmatrix defined in the MEFEL/SRC/alias.h.
The source file of new material class needs to include at the following header files global.h, newmat.h at least. Declarations
of global variables (such as mechmat instance Mm) are given in the global.h. An unique
integer identifier and alias must be assigned to every new material class in the enumeration type mattype
which is defined in the MEFEL/SRC/alias.h. The same alias and corresponding integer identifier should be also added in the enumstr
array mattypestr which is defined in the same include file.
All compulsory functions of the new material class must be called in the switch statements of the corresponding mechmat
procedures where new case with material alias have to be added:
newmat::readhas to be called inmechmat::readmatchar,newmat::matstiffhas to be called inmechmat::matstiff,newmat::nlstresseshas to be called inmechmat::computenlstresses,newmat::updatevalhas to be called inmechmat::updateipvalmat,
mechmat
(MEFEL/SRC/mechmat.h). For example in the case of J2 plasticity, the array Mm->j2f contains
instances of J2 plasticity material with different material constants.
More details about the implementation can be found in source files of material models. The isotropic elastic model is defined in the MEFEL/SRC/elastisomat.h|cpp files, J2 plasticity model is defined in MEFEL/SRC/j2flow.h|cpp and scalar isotropic damage model is defined in MEFEL/SRC/scaldam.h|cpp. Should be also noted that there are other useful classes and functions which provides basic matrix, tensor and vector algebra. They are defined in GEFEL/matrix.h|cpp, GEFEL/tensor.h|cpp and GEFEL/vector.h|cpp.
Implementation of new element
At the beginning, it should be noted that there is strict decomposition of functions and data connected with the finite element method (stiffness matrix, strain-displacement matrix, internal force evaluation, etc.) which are matter of MEFEL and geometrical interpretation of the element which is dealt in GEFEL (nodal coordinates, element connectivity, etc.). The main procedures of all finite elements in the code represent assembling of stiffness matrix of the element, calculation of strains at integration points and calculation of internal forces at nodes resulting from the calculated stresses at the material level (see section with new material implementation). These computations are performed at all elements and they are invoked at solver level by functions defined in the MEFEL/SRC/globmat.cpp.
Compulsory functions in new element class
The finite elements are implemented with help of C++ classes where one type of element is represented by the corresponding class type. Every class of finite element must contain the following compulsory functions:
void newelement::res_stiffness_matrix (long eid, matrix &sm);- assembles the stiffness matrix of the given element,eidis the element number andsmis the resulting stiffness matrix. The stiffness matrix of the finite element in mechanics is defined as:
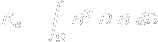
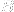 is the strain-displacement matrix and
is the strain-displacement matrix and
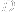 is the material stiffness matrix and
is the material stiffness matrix and
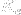 is the stiffness matrix of the element. The matrix
is the stiffness matrix of the element. The matrix
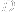 can be obtained at the given integration point with help of
can be obtained at the given integration point with help of
mechmatclass by the call ofMm->matstiff(dm, ipp);void newelement::res_ip_strains (long lcid, long eid);- calculates strain vectors corresponding to actual displacement vector r at all element integration points for the given load case. Argumentlciddenotes the load case number andeidis the element number. The strains are defined as:

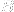 is the strain-displacement matrix,
is the strain-displacement matrix,
 is the vector of nodal unknowns and
is the vector of nodal unknowns and
 is the strain vector in engineering notation.
is the strain vector in engineering notation.void newelement::res_internal_forces (long lcid, long eid, vector &ifor);- calculates nodal internal forces according to the actual stresses at integration points of the given element and for the given load case.Argumentlciddenotes the load case number,eidis the element number andiforis the resulting nodal force vector. The vector of internal forces is defined as:
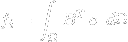
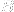 is the strain-displacement matrix,
is the strain-displacement matrix,
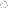 is the stress vector and
is the stress vector and
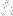 is the vector of stress resultants. It is expected that solver has
already provided the calculation of the strains but the computation of actual stresses at integration points must be
provided in this function.
is the vector of stress resultants. It is expected that solver has
already provided the calculation of the strains but the computation of actual stresses at integration points must be
provided in this function.
Strongly recommended functions in new element class
The following functions represent common decomposition of the previous functions and it is strongly recommended to
implement them:
void newelement::compute_nlstress (long lcid, long eid, long ri, long ci);- computes stress vectors at all integration point of element. Argumentlciddenotes the load case number,eidis the element number,riis the row index of the integration point block calculated andciis the column index of the integration point block calculated. The function is used for the internal forces computation and it should callMm->computenlstressesfunction for all integration points of the given block on element to obtain the stresses (for details aboutMmsee the previous section). The integration point blocks are used in the case of different integration order for some stress components.The blocks are numbered from 0. If this feature is not used there is one block defined only, both indices would be 0 and they may be ignored.void newelement::res_ip_stresses (long lcid, long eid);- computes stress vectors at all integration point of element. Argumentlciddenotes the load case number andeidis the element number. The function is used for the output purposes and it may callMm->computenlstressesfunction for all integration points of element to obtain the stresses (for details aboutMmsee the previous section).void newelement::elem_integration (integratedquant iq, long lcid, long eid, long ri, long ci, vector &nv);- integrates the stress resultants over the element volume. Argumentiqdenotes the integrated quantity (see MEFEL/SRC/alias.h -enum integratedquant). It determines which quantity should be obtained from the integration points and integrated, e.g.iq=local_stressresults to the integration nodal forces due to total stresses in case of local models. Argumentlciddenotes the load case number,eidis the element number,riis the row index of the integration point block calculated andciis the column index of the integration point block calculated. The integration point blocks are used in the case of different integration order for some stress components. The blocks are numbered from 0. If this feature is not used there is one block defined only, both indices would be 0 and they may be ignored. The last output argumentnvis the vector of nodal values of integrated quantity, e.g. nodal forces. The function is called ininternal_forcesfunction family where the nodal forces are defined as:
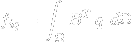
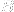 is the strain-displacement matrix,
is the strain-displacement matrix,
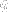 is the vector of integrated quantity and
is the vector of integrated quantity and
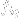 is the resultant vector of given quantity.
is the resultant vector of given quantity.void newelement::transf_matrix (ivector &nodes, matrix &tmat);- assembles the transformation matrix from local nodal coordinate system to the global coordinate system x_g = T x_l. The function should be called inres_stiffness_matrixandres_internal_forcesin order to transform the resulting matrix or vector to the nodal local coordinate systems and inres_ip_strainsshould be called due to transformation of vector of actual nodal unknowns from the nodal local systems to the global coordinate system.
Strongly recommended data members in new element class
Additionally, the class should contain the following data members:
- long ndofe - the total number of degrees of freedom on element,
- long nne - number of nodes on element,
- long ned - number of edges on element,
- long nned - number of nodes on one edge,
- long tncomp - total number of components of stress and strain tensors,
- long *ncomp - array containing numbers of components,
- long *cncomp - array of cumulative numbers of components,
- long napfun - number of approximated functions on the element,
- long **nip; - 2 dimensional array which corresponds to block structure
of integration points.
nip[i][j]defines the number of integration points used in the i,j-th block. - long tnip - total number of integration points on element,
- long **intordsm - 2 dimensional array which corresponds to block structure
of integration points.
intordsm[i][j]defines the order of integration used in the i,j-th block for the stiffness matrix. - long nb - number of blocks of integration points. The integration point blocks are used in the case of different integration order for some stress components. If this feature is not used there is one block defined only.
- strastrestate ssst - defines stress/strain state of the element (see
enum strastrestatein MEFEL/SRC/alias.h).
Recommended functions in new element class
Recommended functions for implementation that allows for volumetric and edge or surface load on elements:
void newelement::res_load_matrix (long eid, matrix &lm);- assembles load matrix of the given element,eidis the element number andlmis the resulting load matrix. The load matrix is defined as:
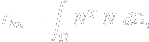
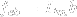
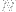 is the matrix of shape functions,
is the matrix of shape functions,
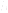 is the vector of nodal values of body force components,
is the vector of nodal values of body force components,
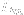 is the load matrix and
is the load matrix and
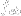 is the resulting load vector due to body forces. It is
assumed that the body forces are approximated by the same shape functions as the nodal unknowns. The function is used
in computations of contributions to load vector due to body forces and without its implementation, only Dirichlet
boundary conditions (i.e. nodal forces or prescribed displacements) can be used.
is the resulting load vector due to body forces. It is
assumed that the body forces are approximated by the same shape functions as the nodal unknowns. The function is used
in computations of contributions to load vector due to body forces and without its implementation, only Dirichlet
boundary conditions (i.e. nodal forces or prescribed displacements) can be used.
void newelement::nodeforces (long eid, long *le, double *nv, vector &nf);- assembles the nodal values of load vector due to edge or surface load. Argumenteidis the element number,leis the array of indicators of load on particular edges/surfaces,nvis the array of nodal edge/surface load components andnfis the output array of the resulting load vector. The vector is defined as:
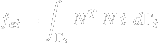
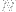 is the matrix of shape functions,
is the matrix of shape functions,
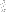 is the vector of nodal values of traction force components
and
is the vector of nodal values of traction force components
and 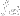 is the load vector due to traction forces.
It is assumed that the traction forces are approximated by the same shape functions as the nodal unknowns.
is the load vector due to traction forces.
It is assumed that the traction forces are approximated by the same shape functions as the nodal unknowns.
Collaboration with mechtop class and GEFEL library
There are several families functions that may or have to be used in the implementation of the above functions.
The user needs to obtain nodal coordinates and node numbers of the element at least. Additionally, there is support
for shape functions and their derivatives. There is also support for the Gauss numerical integration. Element
connectivity and nodal coordinates can be obtained with help of global variable Mt of
class mechtop. The following list of mechtop member functions should be exploited:
void mechtop::give_elemnodes (long eid, ivector &nodes);- returns node numbers of the given element. The argumenteidrepresents element number and output argumentnodesis the integer vector of node numbers.void mechtop:: give_node_coord1d (vector &x, long eid); - returns x coordinates of
element nodes. The output argument void mechtop::give_node_coord2d (vector x, vector y, long eid);- returns x and y coordinates of element nodes. The output argumentsxandyare vectors of coordinateseidis the element number. The xy plane is default for plane and 2D bar elements.void mechtop::give_node_coord2dxz (vector &x, vector &z, long eid); - returns x and z coordinates of element nodes. The output argumentsxandzare vectors of coordinateseidis the element number. The xz plane is default for 2D beam elements.void mechtop::give_node_coord3d (vector &x, vector &y, vector &z, long eid);- returns spatial coordinates of element nodes. The output argumentsx,yandzare vectors of coordinates,eidis the element number.void mechtop::give_nodal_coord (long nid, vector &c);- returns spatial coordinates of the given node. The argumentnidis the node number andcis the vector of coordinates.
x is the vector of x coordinates and eid is the
element number.
It is important to note that in every node, a local coordinate system can be defined. The call of mechtop
function Mt->locsystems(nodes) returns the number of local coordinate systems defined at nodes. The
argument nodes is the integer vector of element nodes that can be obtained by the call
Mt->give_elemnodes(eid, nodes). Usually, the element function transf_matrix assembles
transformation matrix from blocks corresponding to individual nodes. All nodes in the problem are represented by array
of class node in mechtop class. The class node contains data member
transf representing indicator of the local system (transf>0). Base vectors of
the given nodal local coordinate system are stored in data members of class node - e1,
e1, e2 and e3 (e3 is allocated only
for 3D problems).
Every new element class needs to implement function newelement::res_ip_strains which calculates
strains according to actual displacements. The actual displacements are provided by solver used and they can be obtained
with help of void eldispl(long lcid, long
eid, double *r, long *cn, long ndofe);
function defined in global.cpp. The argument lcid is the load case number and eid is the
element number. The output argument r is the pointer to allocated array in which the vector of nodal
displacements of the given element will be returned. The next argument in the list cn is the array of DOF
numbers at element nodes. The last argument ndofe is the total number of DOFs at the given element, i.e.,
it represents length of arrays r and cn.
The implementation of the new finite element requires definition of shape functions and their derivatives. The common definitions of shape functions together with their derivatives can be found in GEFEL files GEFEL/basefunction.cpp and GEFEL/difcalc.cpp. Integrals resulting from the FEM formulation of the problem may be solved numerically with help of Gauss integration formula where the coordinates of integration points and their weights have to be introduced. Some of common natural coordinates and their weights have been already implemented in the GEFEL file GEFEL/intp.cpp. The definition of finite element contains also many vector and matrix operations, see GEFEL files GEFEL/vector.cpp and GEFEL/matrix.h|cpp where many of them have been already implemented.
Adding of references to the new element to other MEFEL files
Every new element must be added in the form of the pointer to the element class in global.h as a new global variable:
EXTERN newelem *Newel;
In the above example, the macro
EXTERN handles the adding of C++ keyword extern
automatically. The declaration/definition of global variable type of pointer to the new element class
newelem follows the macro EXTERN. The corresponding class header file newelem.h
have to be included in the elemhead.h file.
An unique integer identifier and alias must be assigned to every new element class in the enumeration type
elemtype which is defined in the MEFEL/SRC/alias.h. The same alias and corresponding integer identifier
should be also added in the enumstr array elemtypestr which is defined in the same include file.
alias.h.
The global variable defined as the pointer to new element class is initialized in the function read
of class element. The function contains large switch over all implemented elements where, if not done, the
new instance of element class have to be assigned to the global variable pointer.
Additionally, new cases with corresponding code for the new element have to be added to the switch statements
of the following mechtop functions:
long mechtop::give_ndofe (long eid);- returns the total number of degrees of freedom of the given element,long mechtop::give_nne (long eid);- returns the number of nodes of the given element,long mechtop::give_nip (long eid, long ri, long ci);- returns the number of integration points in the given block of integration points of the given element,long mechtop::give_intordsm (long eid, long ri, long ci);- returns the numerical integration order of the given block of stiffness matrix for the given element,long mechtop::give_tnip (long eid);- returns the total number of integration points defined at the given element,long mechtop::give_ncomp (long eid, long bid);- returns the number of stress/strain components in the given block stress/strain block for the given element,long mechtop::give_tncomp (long eid);- returns the total number of stress/strain components,long mechtop::give_ned (long eid);- returns the number of element edgeslong mechtop::give_nned (long eid);- returns the number of nodes on one edge,long mechtop::give_nsurf (long eid);- returns the number of surfaces of the given element,long mechtop::give_nnsurf (long eid);- returns the number of nodes of one element surfacelong mechtop::give_napfun (long eid);- returns the number of shape functions,long mechtop::give_dimension (long eid);- returns the dimension of element (1,2 or 3),long mechtop::give_nb (long eid);- returns the number of integration point blocks on which the stress/strain vector is decomposed,
eid represents element number, ri and
ci are row and column indices of the required integration point block (see
elem_integration function for more details). Similarly, the argument
bid represents block of stress/strain components corresponding that results from the decomposition of
the integration point blocks.
New cases with calls of key class functions have to be also involved in switch statements of
the following functions in MEFEL/SRC/elemswitch.cpp:
void stiffmat(long lcid, long eid, matrix &sm);- add call toNewel->res_stiffness_matrix(eid, sm)void compute_ipstrains (long lcid);add call toNewel->res_ip_strains(eid, lcid)void compute_ipstresses (long lcid);add call toNewel->res_ip_stresses(eid, lcid)void elem_internal_forces (long i, long lcid, vector &ifor);add call toNewel->res_internal_forces(lcid, eid, ifor)void elem_nlstresses (long i, long lcid);add call toNewel->compute_nlstress(lcid, eid, 0, 0)
Recommended functions in new element class for higher functionality
The new class of element should define the following functions in case that higher functionality is required with respect to the output, eigenstrains, nonlocal and time dependent models or coupled models.
void newelement::compute_nodestrains (long lcid);- computes strains at nodes (due to output)void newelement::computestrains (long lcid);- general function for strain computations (due to output)void newelement::compute_nodestresses (long lcid);- computes stresses at nodes (due to output)void newelement::computestresses (long lcid);- general function for stress computation (due to output)void newelement::compute_nodeothers ();- computesothervalues at nodes (due to output)void newelement::elem_eigstrain_forces (long lcid, long eid, vector &nfor);- computes forces due to eigenstrains (eigenstrains and temperature load)void newelement::elem_intpointval (long eid, vector &nodval, vector &ipval);- computes integration point values from nodal transport quantities on linear elements (due to coupled models of mechanics and transport problems)void newelement::elem_intpointval2 (long eid, vector &nodval, vector &ipval);- computes integration point values from nodal transport quantities on quadratic elements (due to coupled models of mechanics and transport problems)void newelement::elem_mechq_nodval (long eid, vector &nodval, nontransquant qt);- returns values of selected mechanical quantities at integration points (due to coupled models of mechanics and transport problems)double newelement::interpolate (long eid, double *nodval, double *coord);- computes interpolates nodal values on the given element to the point with given natural coordinatesvoid newelement::ipvolume();- computes ratio of element volume corresponding to particular integration points (due to nonlocal models)void newelement::elem_local_values (long i, long lcid);- computes local values at integration points (due to nonlocal models)void newelement::elem_nonloc_internal_forces (long i, long lcid, vector &ifor);- computes local values at integration points (due to nonlocal models)void newelement::elem_incr_internal_forces (long i, long lcid, vector &ifor);- computes increments of internal forces due to increment of irreversible strains (due to time dependent models)void newelement::massmat (long lcid, long eid, matrix &mm);- computes mass matrix (due to dynamics)void newelement::elem_integration_quant (long eid, integratedquant iq, long lcid, vector &nv);- computes integral over element volume form the nodal values of selected quantities (due to homogenization via macro-stress approach)
switch statements of the corresponding functions in MEFEL/SRC/elemswitch.h|cpp.
More details about the element implementation can be found in source files of individual elements in MEFEL/SRC/ - plelemlt.h|cpp (linear triangular plane element), plelemlq.h|cpp (linear quadrilateral plane element), lintet.h|cpp (linear tetrahedron element), linhex.h|cpp (linear brick element), etc.